Il telescopio spaziale Spitzer, prima del suo lancio – Spitzer Space Telescope, before its launch
Il telescopio spaziale Spitzer, anche se molto meno conosciuto di Hubble, è comunque uno degli strumenti scientifici che hanno dato più risultati negli ultimi anni. Se infatti il campo visuale di Hubble va da�l vicino infrarosso all’ultravioletto, Spitzer raccoglie informazioni da tutta la radiazione infrarossa, quella che, per intenderci, emettono i corpi a bassa temperatura. Lo stesso corpo umano emette raidazioni infrarosse: è come se noi brillassimo come tante lampadine, ma i nostri occhi non possono vedere questa luce.
Beside Spitzer Space Telescope is less known than Hubble, it’s one of the scientific instrument which gave us very important informations during the last years. In fact, Hubble can see only light from the near infrared radiation to ultraviolet one. Instead, Spitzer takes its informations from all the infrared radiation, which is emitted by cold bodies. Human body itself emits infrared radiation: we shine just as like as many light bulbs, but we can’t see our light.
L’utilizzo di queste particolari lunghezze d’onda permette di andare oltre le barriere della luce visibile: un po’ come, utilizzando gli infrarossi, si vedono gli oggetti anche al buio, lo stesso vale per le stelle nelle nebulose: il gas che le nasconde nelle immagini di Spitzer “sparisce”, e così si possono vedere cose altrimenti invisibili.
Using light at this wavelenght make us capable to see beyond barriers of visible light: in the same way that, using infrared light, we can see things in the dark, we can also uncover stars in nebulae: the gas which hides them “disappears” in Spitzer’s images, and so we can see details which otherwise would be invisible.


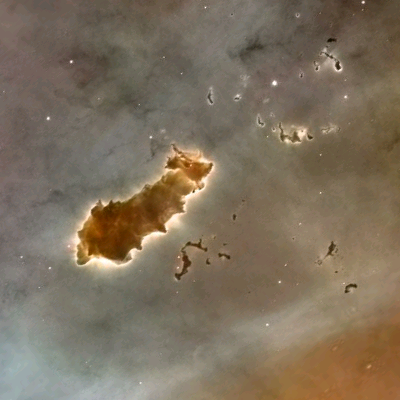
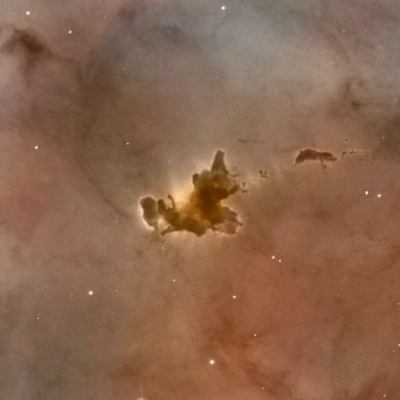
La Nebulosa Aquila vista da Hubble (sopra) e Spitzer (sotto) – Eagle Nebula as it’s seen by Hubble (above) and Spitzer (below)
Come vedete, il gas interstellare che sta formando le stelle nella nebulosa aquila diventa una nebbiolina verde attraverso la quale è possibile vedere ciò che c’è dietro. Ciò che è più importante in quest’immagine, però, è il colore rosso al centro. Il rosso corrisponde ad una regione di gas e polveri molto più calda: qual’è può essere l’origine di questo calore?
As you can see, gas which is forming new stars in eagle nebula becomes a green fog through which we can see what is behind it. But the most important thing in this image is the red color in the centre. Red stands for a region of dust and gas much hotter: what’s the origin of this warm temperature?
Proprio dove ora c’è quel gas, tra gli 8000 e i 9000 anni fa è esplosa una supernova: la sua onda d’urto ha scosso per bene la nebulosa ma, visto che questa dista da noi 7000 anni luce, non abbiamo ancora visto le sue conseguenze. Tra 1000 o 2000 anni (qualdo saremo capaci di vedere la luce che lasciò la nebulosa 6000-5000 anni fà) vedremo l’onda d’urto raggiungere le famose “tre dita” (poco più a destra del centro): queste saranno distrutte e, in un crogiolo di stelle che esplodono, se ne formeranno di nuove. Questa scoperta sarebbe stata impossibile attraverso la luce visibile: non avremmo mai saputo della regione più calda.
Where now there is that hot gas, a supernova exploded 8000-9000 years ago: its shock wave shaked the nebula a lot, but, because of the nebula is 7000 light years from the earth, we have not yet observed its consequences. In 1000 or 2000 years (when we’ll be able to see light that leaved the nebula 6000-5000 years ago), we’ll see the shock wave reaching the famous “three fingers” of the nebula (a bit right from the centre of the image): these will be destroyed and, between exploding stars, many new others will born.
Spero di aver fatto una buona introduzione ad uno strumento di grandissima importanza, che continuerò a seguire come ho fatto per Hubble. Ciao!
I hope I’ve made a well introduction to this very important instrument, that I’ll follow in my website as I actually do with Hubble. Bye!