Vi è mai capitato di seguire con lo sguardo un aeroplano, per qualche minuto? Se l’avete fatto, vi sarete certamente accorti che sembra andare fortissimo quando è proprio sopra la testa, per rallentare poi man mano che si allontana, abbassandosi verso l’orizzonte.
Ma una volta giunto all’orizzonte che accadrà? Di sicuro non si abbatterà al suolo, come l’occhio sembrerebbe suggerire: se l’aereo non è partito da poco, la sua quota sarà più o meno fissa, sui 10 km. Ma se sta ancora volando, sopra a cosa starà volando? Quanto distante sarà?
E se invece di guardare aerei salissimo noi, per quanto possibile, verso il cielo? Se dalla cima di una montagna con una buona visuale, da un picco isolato, da una svettante torre guardassimo lontano, fino a dove si spingerebbe il nostro sguardo? In altre parole, quando è lontano l’orizzonte?

La Terra dallo Spazio – Samantha Cristoforetti
La distanza dall’orizzonte non è un concetto metafisico e sebbene possieda una certa forza evocativa è una quantità fisica precisa. Già gli antichi sapevano che oltre una certa distanza non si vede più niente e che ciò ha poco a vedere con la presenza di nebbie e foschie. Il motivo per cui esiste la linea dell’orizzonte è un altro: la Terra è rotonda.
Sappiamo tutti che le persone che vivono nell’emisfero australe sono capovolte, rispetto a come siamo noi. Naturalmente non hanno la testa in basso: il loro basso è il nostro alto, ecco tutto. Mi viene in mente una striscia di Mafalda, nella quale la bambina argentina appende il suo mappamondo al contrario perché sennò “le cadono le idee dalla testa”…
Anche quando un oggetto, allontanandosi da noi, si sposta sulla superficie terrestre il suo basso cambia rispetto a quello del punto dov’era partito: in altre parole la sua verticale e la nostra iniziano a essere diverse, a formare tra loro un piccolo angolo. Ma così come non possiamo vedere i nostri ribaltati amici neozelandesi, ad un certo punto il nostro sguardo non potrà più scorgere l’oggetto: sarà la Terra stessa, con la sua forma più o meno sferica, a nascondercelo.
 Ma quanto è lontano questo punto, oltre il quale la Terra si nasconde da sola? Il senso comune dice che dipenderà da quanto alti si è: non lo sanno forse tutti che per vedere lontano bisogna salire in alto? La matematica necessaria per trovare la formula corretta è piuttosto semplice, basta solo un po’ di trigonometria. O filosofi e poeti che avete letto sin’ora e che siete assaliti da un cupo timore, se non da un corrucciato fastidio, abbiate la tempra di proseguire! La conoscenza non distrugge il sentimento!
Ma quanto è lontano questo punto, oltre il quale la Terra si nasconde da sola? Il senso comune dice che dipenderà da quanto alti si è: non lo sanno forse tutti che per vedere lontano bisogna salire in alto? La matematica necessaria per trovare la formula corretta è piuttosto semplice, basta solo un po’ di trigonometria. O filosofi e poeti che avete letto sin’ora e che siete assaliti da un cupo timore, se non da un corrucciato fastidio, abbiate la tempra di proseguire! La conoscenza non distrugge il sentimento!
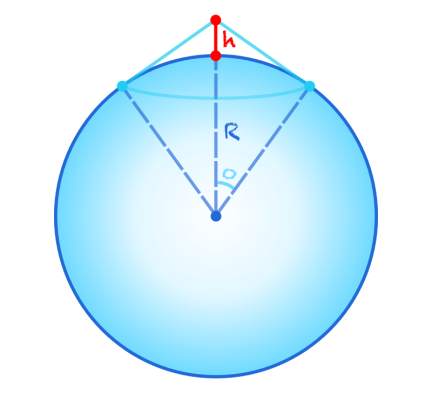
L’angolo che nel disegno è chiamato  è l’angolo massimo oltre il quale uno che guarda dalla cima dell’altezza
è l’angolo massimo oltre il quale uno che guarda dalla cima dell’altezza  non vedrà più niente. Le linee che congiungono la cima di
non vedrà più niente. Le linee che congiungono la cima di  agli ultimi due punti visibili sulla superficie sono segmenti di rette tangenti alla circonferenza; non è difficile rendersene conto: una retta può intersecare un cerchio in un punto, in due, oppure in nessuno. Se la retta che passa per
agli ultimi due punti visibili sulla superficie sono segmenti di rette tangenti alla circonferenza; non è difficile rendersene conto: una retta può intersecare un cerchio in un punto, in due, oppure in nessuno. Se la retta che passa per  interseca due punti, il più vicino è visibile ma ci nasconde il secondo, che quindi è invisibile: guardando per terra vediamo il suolo, ma non l’Oceano Pacifico che ci sta sotto. Se non ne interseca nessuno allora stiamo guardando per aria. L’ultima direzione alla quale corrisponde un punto visibile si ha allora quando la retta interseca la circonferenza in un solo punto, e una tal retta è una tangente.
interseca due punti, il più vicino è visibile ma ci nasconde il secondo, che quindi è invisibile: guardando per terra vediamo il suolo, ma non l’Oceano Pacifico che ci sta sotto. Se non ne interseca nessuno allora stiamo guardando per aria. L’ultima direzione alla quale corrisponde un punto visibile si ha allora quando la retta interseca la circonferenza in un solo punto, e una tal retta è una tangente.
Le tangenti alla circonferenza sono sempre perpendicolari al raggio, nel punto in cui la toccano. Quindi il triangolo formato dal raggio della Terra fino al punto di tangenza, dal segmento  e dal segmento che congiunge l’estremo di h al punto di tangenza è rettangolo.
e dal segmento che congiunge l’estremo di h al punto di tangenza è rettangolo.
Ma allora si può usare un po’ di sana trigonometria per determinare l’angolo  , la cui misura in radianti, moltiplicata per il raggio terrestre R, darà la lunghezza dell’arco di circonferenza tra
, la cui misura in radianti, moltiplicata per il raggio terrestre R, darà la lunghezza dell’arco di circonferenza tra  e il punto di tangenza, ovvero la distanza dell’orizzonte. Se non avete chiuso i vostri libri di matematica in un polveroso scatolone da almeno due secoli, dovrebbe risultarvi chiaro che:
e il punto di tangenza, ovvero la distanza dell’orizzonte. Se non avete chiuso i vostri libri di matematica in un polveroso scatolone da almeno due secoli, dovrebbe risultarvi chiaro che:
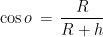
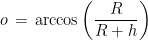

Bene, ecco trovata la formula che stavamo cercando. Ma serve veramente a qualcosa? Conosco un paio di persone che sanno a memoria valori sparsi della funzione trascendente arcocoseno, ma calcolarla a mente richiede un po’ di conti noiosi. Meglio fare un’approssimazione e accontentarci di una formula inesatta, che compie qualche errore, ma è più semplice da maneggiare. Del resto, a chi importa se una nave invece di essere distante 10 km, è distante 10 km e 2 cm??
Devo confessarvi che non ricordo mai lo sviluppo in serie di potenze della funzione arcocoseno. Potrei sempre ricavarlo, ma lasciatemi seguire una strada meno irta di derivate: tanto sono certo che un giorno pagherò cara anche questa. Ripartiamo dalla prima equazione, quella in cui è presente il coseno di  . Del coseno mi ricordo lo sviluppo!
. Del coseno mi ricordo lo sviluppo!
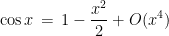
Del resto anche il membro di destra può essere rimaneggiato, in modo da essere scritto:

Ma posso sviluppare anche questo:

Siccome il raggio della Terra è 6373 km, ogni altezza terrestre (e anche qualche altezza spaziale) è piccola rispetto ad esso. Mi arresto, dunque, al primo termine non costante degli sviluppi, e riscrivo l’equazione in forma approssimata:

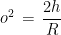

Ma la distanza sulla superficie, cioè la lunghezza dell’arco di circonferenza, è 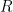 volte l’angolo
volte l’angolo  …
…


Ecco fatto: la distanza dell’orizzonte è, in prima approssimazione, la radice del prodotto tra il diametro terrestre 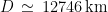 e l’altezza da cui si guarda, ovvero, se qualcuno si ricorda ancora cos’è, la loro media geometrica. Una radice quadrata è più semplice da calcolare di un arcocoseno, ed ecco la più immediata utilità della formula approssimata.
e l’altezza da cui si guarda, ovvero, se qualcuno si ricorda ancora cos’è, la loro media geometrica. Una radice quadrata è più semplice da calcolare di un arcocoseno, ed ecco la più immediata utilità della formula approssimata.
Del resto, che approssimata lo sia appare chiaro se si considera il suo limite superiore: se uno andasse a una distanza grandissima dalla Terra, per la formula dovrebbe vederne una parte sempre più grande man mano che si sposta. Invece non è così: per quanto uno possa allontanarsi, non vedrà mai più di un emisfero contemporaneamente e il “retro” resterà sempre nascosto, proprio come della Luna non potremo mai vedere l’altra faccia, a meno di non girarle attorno.
Ma qual è l’errore che si fa quando si usa la formula? Ecco una tabellina con dei valori di altezze e di distanze degli orizzonti, per fare qualche confronto:
| Chi/Cosa |
h |
d (radice) |
d (arccos) |
| Naufrago in mezzo all’oceano |
2 cm |
509 m |
509 m |
| Formica in cima a un filo d’erba |
10 cm |
1,13 km |
1,13 km |
| Giovanni nella prateria |
1,7 m |
4,65 km |
4,65 km |
| In cima all’albero di un veliero |
20 m |
15,97 km |
15,97 km |
| Campanile di San Marco |
100 m |
35,7 km |
35,7 km |
| Monte Priaforà |
1659 m |
145,41 km |
145,40 km |
| Monte Everest |
8848 m |
335,82 km |
335,63 km |
| Aereo di linea |
10 km |
357,0 km |
356,8 km |
| Stazione spaziale |
400 km |
2258 km |
2201 km |
| Luna |
384400 km |
70000 km |
9907 km |
L’errore massimo (per uno che guarda dalla stazione spaziale) è circa del 2,5%! La formula approssimata è molto conveniente. Amenoché non si tenti di usarla per sapere come vede la Terra la quieta Luna. In questo caso la “quota” dalla superficie non è più piccola rispetto al raggio terrestre e l’approssimazione cade: la formula semplice fornisce un risultato assurdo, maggiore della circonferenza del pianeta, mentre quella con l’intera funzione arcocoseno dà un valore corretto, che si avvicina a  , un quarto di circonferenza terrestre.
, un quarto di circonferenza terrestre.

E voi, cosa aspettare a salire in alto per guardare lontano?