Quando non ho niente da fare, capita che scovi qualche strano risvolto di una formula o che inventi e risolva (se ci riesco) alcuni problemi di tipo fisico/matematico. Questo tipo di comportamento è considerato dai siòri con cui mi confronto ogni giorno anormale, abnorme, rivoltante, abominevole, infantile, psicotico, se non semplicemente ridicolo e sintomo di un’incapacità mentale più o meno vasta. Desidero dedicare a tutte queste belle persone, ed ad una in particolare, questo post.
Avevamo appena concluso lo studio delle matrici a scuola. Delle matrici non sapevo niente, e anche se le trovavo piuttosto noiose, mi piaceva il concetto di determinante e di rango: due numeri coi quali si possono individuare caratteristiche comuni in matrici differenti. La parte più interessante era stata la scoperta che tramite le matrici quadrate di ordine 3 si potevano rappresentare tutte le coniche, le curve studiate l’anno precedente.
Una mattina la lezione era noiosa e così mi son messo a moltiplicare le matrici tra di loro. Mi son accorto che moltiplicando la matrice “circonferenza di raggio 1” per se stessa si otteneva la matrice identità:

Pensai che fosse una cosa interessante. Si otteneva la stessa cosa anche moltiplicando per se stessa la matrice “iperbole equilatera”: entrambe le matrici erano le reciproche di se stesse. Iniziai a chiedermi cosa potesse rappresentare la matrice identità, vista come conica: traducendo la matrice in equazione si ottiene:
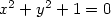
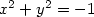
Trovai la cosa interessante: interessante, non impossib ile. Infatti avevo già studiato in numeri complessi. Perché non provare a risolvere la cosa addentrandosi nel misterioso mondo dei numeri immaginari? Sviluppai il mostro come di seguito:
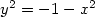
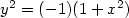
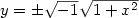
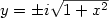
A questo punto ho pensato che avrei potuto dare alla variabile indipendente anche valori complessi. In quest’ottica, sarebbe stato comodo spaccarla in parti reale ed immaginaria, così ho trasformato l’equazione precedente in:
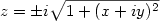
Dove “z” è, chiaramente, un numero complesso. Ma c’è un problema: per rappresentare l’oggetto descritto dall’equazione ci vogliono 4 dimensioni! Due servono per i valori in ingresso (x,y) e due per i valori in uscita (z reale, z immaginario). Peccato che il mio universo ne abbia solo 3 e che i miei occhi ne vedano 2! Che delusione!!
Non perdendomi d’animo, pensai di tagliare l’iperspazio quadrimensionale dove viveva il mostro conico con uno spazietto tridimensionale a cui sono più abituato. Cosa succede, ad esempio, se annullo la y? La mia equazione si riduce a:
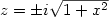
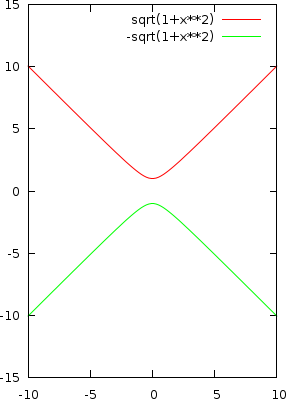
Osservandola, si nota che la radice può assumere solo valori reali, che moltiplicati per l’unità immaginaria danno solo valori immaginari. Con y=0 , dunque z assume soltanto valori immaginari! Guardandola ancora meglio, si nota che la forma, a meno della “i” è la stessa di quella di un’ iperbole equilatera con l’asse trasverso coincidente con l’asse delle y. In altre parole, la funzione, per y=0, ha questa forma:
Mi sono poi chiesto cosa sarebbe successo se avessi annullato la x, intersecando quindi la mostruosa iperconica con lo spazio x=0 . L’equazione, dopo aver elevato l’unità immaginaria al quadrato, diventa:
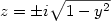
Succede adesso una cosa interessante. Se y è minore di 1 e maggiore di -1, l’equazione, sempre a meno di “i”, è della stessa forma di quella di una circonferenza di raggio uno. Anche questa volta, i valori assunti da z saranno tutti immaginari, e, dunque, la funzione avrà il grafico di una circonferenza nell’intervallo [-1,1].
Ma se i valori della y sono esterni all’intervallo ]-1,1[ , allora il radicando è negativo. Possiamo dunque raccogliere un -1 dal radicando:
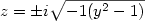
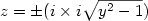
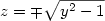
Stavolta i valori assunti da z sono tutti reali, e il loro grafico coincide con quello di un’iperbole con l’asse trasverso coincidente con l’asse delle x:
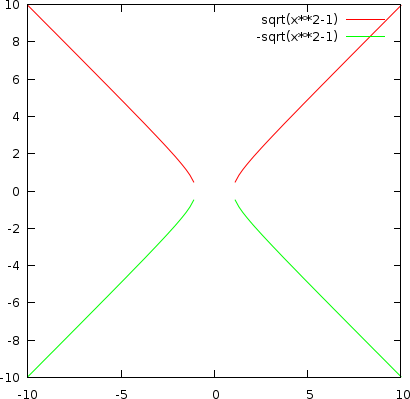
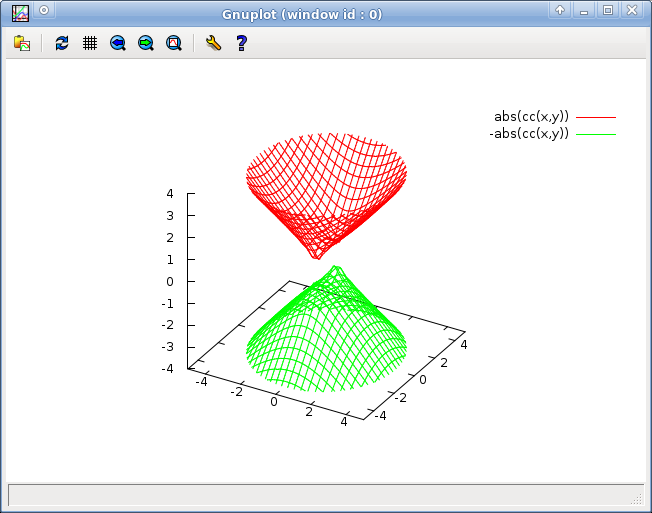
Ottenuti questi risultati, mi sono chiesto se c’era un sistema per vederli tutti insieme, estraendo le informazioni dalla funzione. Ho provato vari metodi, ma il migliore, per visualizzare queste caratteristiche, è risultato essere la funzione seguente.
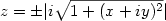
Il modulo evita lo spiacevole inconveniente della quarta dimensione, associando a z solo un singolo numero reale: il modulo del numero complesso, appunto. Riporto qui sotto il grafico, che ho evidenziato aggiungendo delle ombre in matita:
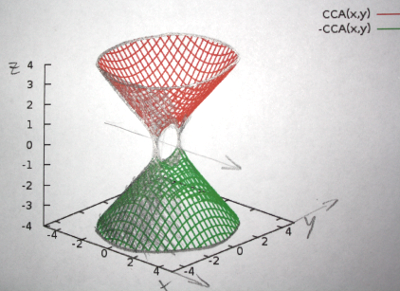
Da questo punto di vista, è possibile vedere bene la circonferenza di raggio unitario (che assumerebbe valori immaginari) e l’iperbole “orizzontale” (che assumerebbe valori reali) sul piano yz. Dando un’occhiata al piano xz, invece, si vede che l’oggetto è una specie di iperboloide a due falde: l’iperbole intersecato da questo piano è quello “verticale” che abbiamo trovato per primo (che assumerebbe valori immaginari).
Arrivato a questo punto, mi sono detto soddisfatto. In gran parte lo sono stato perché ero riuscito a prevedere alcune interessanti caratteristiche dell’oggetto senza adoperare il computer. Ho poi portato i risultati al professore, col quale avevo discusso la cosa durante la ricreazione.
All’oggetto soprastante si potrebbe affiancarne anche un altro: quello che associa ad ogni punto (x,y) l’anomalia del numero complesso z: utilizzando i due grafici in maniera coordinata, si potrebbe avere un’idea d’insieme della mostruosa iperiperbole, anche senza vederla. Ma adesso sono stanco!!