La settimana scorsa ho fatto un giro nel mio liceo, per salutare (leggasi “rompere le scatole”) qualche vecchio professore. Il buon Aldo Neresini, professore di Fisica, mi ha domandato se conoscessi un paradosso relativistico relativo a uno sciatore che casca (o forse no?) dentro un buco. In altri termini, l’apparente paradosso è questo:
Un’asta lunga L scivola senza attrito su una lamina, che si può pensare come un piano infinitamente sottile. La lamina è perforata e il foro è lungo esattamente L. Per un osservatore solidale con il piano, la barra è lunga meno di L, in ragione di 1/γ, a causa della contrazione relativistica delle lunghezze. L’osservatore solidale con la lamina conclude che prima o poi, essendo più corta del buco, l’asta ci cadrà dentro. Viceversa, in un sistema di riferimento solidale con l’asta, questa misurerà L e sarà il foro ad essere contratto fino a L/γ. Ma allora la barra non può cascarci dentro, se è più lunga! Chi ha ragione?
Questa contraddizione (che in realtà non c’è) salta fuori perché siamo portati a pensare all’asta come un oggetto la cui rigidità è indipendente dal sistema di riferimento. Ma in relatività ristretta non è così, anzi, non si può nemmeno dare una vera e propria definizione di corpo rigido!
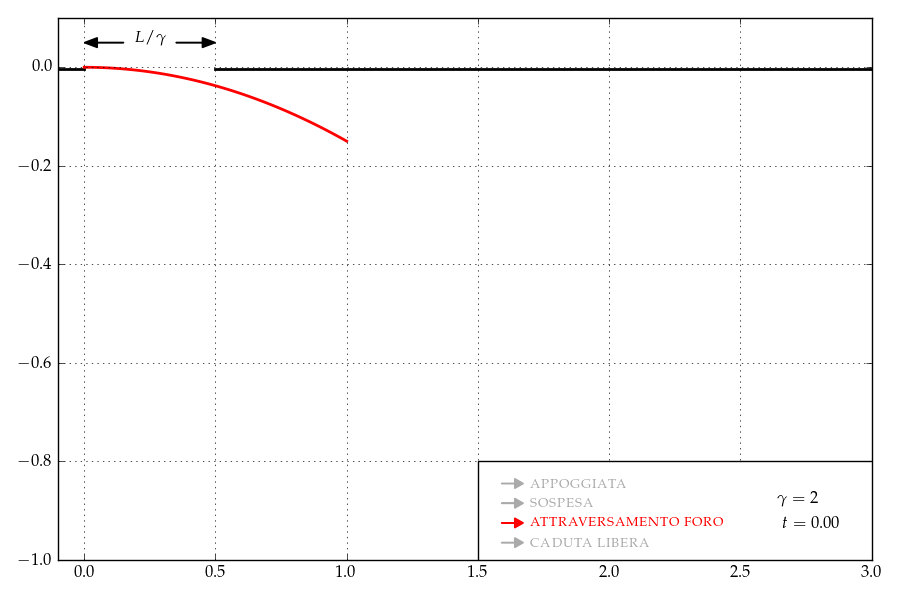
La caduta dell’asta nel sistema di riferimento ad essa solidale prima che inizi ad accelerare. L’asta si deflette e attraversa il foro, anche se è più corto di lei.
Sorprendentemente, la descrizione corretta (con alcuna assunzioni iniziali) è quella data dall’osservatore solidale col il piano d’appoggio, ossia che la sbarra cade nel buco. Nel sistema di riferimento solidale col moto uniforme dell’asta essa non obbedisce al vincolo di rigidità e si deflette, passando per il foro. L’estremo anteriore, in questo riferimento, è il primo a cadere, quando ha già oltrepassato il margine del foro e mentre la parte posteriore della barra è ancora appoggiata sul piano. Successivamente, anche tutti gli altri punti iniziano a cadere, ma a istanti di tempo differenti l’uno dall’altro. Globalmente, il moto dell’asta ricorda quello del metallo che esce da un laminatoio a caldo…
I conti che permettono di derivare questo risultato sono riassunti in questo documento: Il tombino relativistico. Ho scritto anche uno script in Python/Matplotlib che permette di visualizzare il fenomeno al variare del parametro γ dell’asta e genera dei video o delle animazioni interattive. Potete trovare tutto questo materiale, e un collegamento a un articolo del 1961 di W. Rindler (quello delle coordinate del moto accelerato) a questo indirizzo: materiale aggiuntivo. Non mi resta che aggiungere un video, per farvi vedere come fa la sbarra ad attraversare il foro!

Giovanni Ceribella
Sull’ottimo sito http://www.vialattea.net è presente una risposta al medesimo quesito del prof. Nicola Fusco (omonimo dell’analista autore della “Analisi Matematica 2” assieme a Marcellini e Sbordone). Ecco il link alla risposta: http://www.vialattea.net/esperti/php/risposta_printable.php?num=10535. Il prof. Fusco deriva, sulla base del tempo di trasmissione dei segnali luminosi, una risposta opposta a quella presentata qui e condivisa dall’articolo di W. Rindler del 1961.
Temo che la radicale differenza nel fenomeno derivi dalla simili, ma diverse, semplificazioni operate per tener conto della gravità. L’articolo di Rindler, in questo senso, specifica che la stessa fenomenologia (la barra che si curva nel sistema di riferimento in moto con essa) si potrebbe applicare anche ad un qualunque tipo di spinta, non necessariamente di natura gravitazionale.
Questo paradosso si fa sempre più intricato… cercherò di mettermi in contatto col professor Fusco per far luce sulla questione.