Il 9 maggio scorso il tempo sull’Italia settentrionale era pessimo: era in transito una perturbazione di provenienza atlantica e sulle prealpi la copertura nuvolosa era pressoché totale. Per riuscire a vedere il transito di Mercurio, un fenomeno relativamente raro che consiste nel passaggio del piccolo pianeta davanti al Sole, ho fatto una breve gita in Germania, valicando le Alpi e sorpassando le nuvole in volata. Appena finirò di elaborare le immagini pubblicherò un resoconto dell’escursione.
Tornato a casa, si è posto il problema di come utilizzare il materiale raccolto. Mi sono concentrato su un breve video, della durata di 8 minuti circa, che riprendeva Mercurio mentre passava vicino a un gruppo di macchie solari. Il filmato era stato girato alla velocità di 50 fotogrammi al secondo, ma ciascuno di essi era disturbato dalla turbolenza atmosferica, che impediva di scorgere i dettagli dell’inquadratura. In casi come questo di solito si mediano più fotogrammi per ottenerne uno solo, in cui gli effetti di distorsione sono ridotti. Per fare ciò bisogna che tutti i fotogrammi siano prima riallineati nel modo più preciso possibile.
L’allineamento delle fotografie astronomiche che riprendono campi stellari è relativamente semplice: bisogna far corrispondere le immagini delle stelle in un’immagine alle immagini delle stesse stelle di un’altra. Con delle foto della superficie solare ad alto ingrandimento, la scarsità e la variabilità dei dettagli rendono l’operazione più difficile. Cercando in rete ho trovato un algoritmo generico abbastanza semplice che può essere d’aiuto. Funziona così: di ciascuna immagine si calcola la trasformata di Fourier bidimensionale discreta e si costruisce lo spettro di potenza incrociato:
Qui è il momento associato a
che descrive le immagini bidimensionali.
Così come lo spettro di potenza di un segnale è la trasformata della funzione di autocorrelazione, si può mostrare che lo spettro di potenza incrociato è la trasformata della funzione di correlazione incrociata (o cross-correlazione):
Quando uno ha per le mani la funzione di correlazione incrociata “er ist fertig”, almeno in teoria. Infatti, in linea di principio, se le due immagini fossero l’una la traslazione rigida dell’altra la cross-correlazione avrebbe un picco di intensità alle coordinate corrispondenti al vettore di traslazione. In altre parole, quando si ha la cross-correlazione si sa di quanto spostare la seconda immagine per allinearla alla prima.
Tradurre in una tecnica pratica i risultati di qualche calcolo non è mai un’operazione immediata. Per allineare i fotogrammi ho scritto uno script in Python (potete scaricarlo al termine dell’articolo) che include questi passaggi:
- Le immagini sono ridotte in bianco e nero e la scala dei colori è invertita, in modo che il dettaglio più evidente (il disco di Mercurio) risulti molto luminoso su uno sfondo scuro. Le due immagini da allineare sono ricampionate alla metà della loro dimensione originaria (bin 2×2), per ridurre gli effetti della turbolenza.
- A ciascuna viene applicata una maschera gaussiana con 4px di sigma per distruggere eventuali difetti puntuali dell’immagine. Si trova il massimo d’intensità delle due immagini. Questo corrisponde pressapoco al centro del disco di Mercurio (X,Y).
- Attorno alle coordinate (2X,2Y) di ciascuna immagine originale (non ricampionata) si ritaglia un quadrato di 128 pixel per lato. Questa misura è comoda perché è una potenza di 2 ed è sufficiente, nel mio caso, a contenere l’intero Mercurio. Dei due quadrati si trova la funzione di correlazione incrociata, come descritto in precedenza.
- La funzione di cross-correlazione può essere interpretata essa stessa come un’immagine quadrata di dimensione 128×128 pixel. Se ne trovano le coordinate del massimo assoluto e tali valori sono usati per far partire un fit gaussiano del picco d’intensità, che fornisce la posizione del massimo con precisione sub-pixel (x,y).
- L’immagine originale è traslata della quantità non intera (-2X-x,-2Y-y) e ricampionata alla griglia dei pixel della prima immagine interpolandola con una spline cubica.
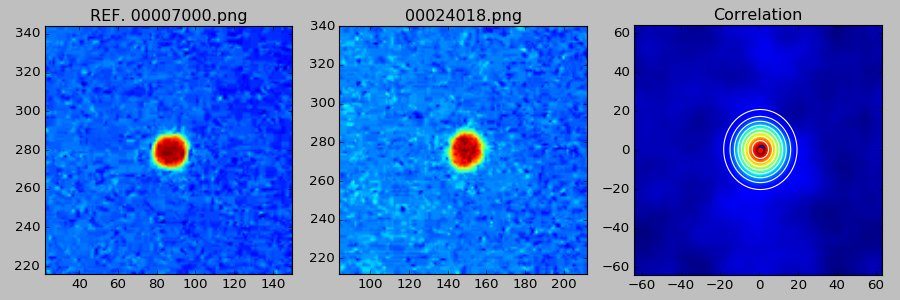
La schermata informativa del programma “Flecken”. Con una scala di colori modificata, sono visibili l’immagine di referenza, quella da allineare, l’immagine di cross-correlazione col contorno del fit gaussiano.
È finita? Certamente no, a questo punto bisogna suddividere i fotogrammi in gruppi omogenei e mediarli. Chiaramente ciascun gruppo di fotogrammi non può contenerne più di un certo numero, perché col tempo che passa il pianeta si sposta! Nel mio caso i fotogrammi erano 24018 e li ho suddivisi in gruppi da 250 l’uno, ottenendo 96 immagini finali mediate. La media è stata fatta con una funzione che pure avevo scritto in precedenza e che fa parte di una minuscola libreria in Python dove ho raccolto un po’ di operazioni utili per manipolare le immagini, gcim.
Alla fine del circo, l’algoritmo di allineamento ha riallineato tutti i 24018 fotogrammi: in 5 casi (0,02% del totale) il fit gaussiano non è andato a buon fine e si è usata una traslazione con precisione al pixel intero; in 66 casi (0,27% del totale) il fit gaussiano è converso ad un valore abnorme, probabilmente a causa di un gradiente lineare sottostante al picco gaussiano. L’identificazione di questi 66 casi è stata possibile grazie al registro dove lo script salva tutti i dettagli di cosa fa. Sto ancora pensando a un modo per permettergli di riconoscere automaticamente questi casi.

Confronto tra due fotogrammi non allineati. Il pianeta e le macchie solari sono in posizioni diverse.

Confronto tra i fotogrammi precedenti dopo l’allineamento. Il pianeta è ora fisso nella stessa posizione.
Alla fine ho usato un programma libero, ImPPg (che pure, volendo, implementa una procedura simile per l’allineamento delle immagini) per applicare dei filtri di deconvoluzione alle immagini risultanti. Ho quindi rimontato un piccolo video accelerato, che aggiungerò presto su questo sito.
Infine, ecco lo script di allineamento: ne ho prodotto due versioni, rispettivamente “Fleck” e “Flecken”. Il primo allinea due immagini, salvando una versione traslata della seconda per farla coincidere con la prima. Il secondo fa la stessa cosa ma in modo sequenziale, lavorando su una lista di immagini da allineare. Per eseguirli avete bisogno di un’installazione di Python con i moduli Numpy, Scipy, Matplotlib. Serve anche la mia piccola libreria gcim, che è già inclusa assieme agli script. Potete scaricare tutto da qui.
Francamente, dubito che il programma, così com’è, possa servire a qualcuno per allineare le sue immagini. Non so nemmeno come si comporti con dei fotogrammi diversi da quelli del video per il quale l’ho scritto. Ma di certo può essere un buon punto di partenza, se qualcuno ha voglia di lavorarci un po’ su.
A presto!

Lascia un commento