Il Compasso Iperbolico (2)

Non avrei mai pensato che, dopo tanto tempo, sarebbe saltato fuori qualcuno a cui interessa il piccolo strumento per disegnare archi d’iperbole che ho costruito nel lontano 2007. Invece sembra che a Maurizio interessi, quindi ho scritto questo piccolo post per spiegargli come funziona.

Vanno fatte alcune doverose precisazioni:

• Lo strumento, a causa del suo stesso progetto, può disegnare archi d’iperbole molto corti e distanti dall’asse trasverso della conica;
• La struttura del compasso è poco stabile e facilmente soggetta a rotture: ciò è riconducibile alla lavorazione molto pressapochista che ne avevo fatto, utilizzando strumenti e materiali non adatti allo scopo;

Ad ogni modo, la struttura del compasso si basa sulla definizione di iperbole: il luogo geometrico dei punti del piano tale che per ogni punto la differenza delle sue distanze da due punti fissi detti fuochi è uguale ad una costante. Ho creato una pagina web con una applet Java che permette di visualizzare il tutto: potete trovarla su http://gio27.altervista.org/iperbole.html , il mio contenitore di contenuti multimediali vari…

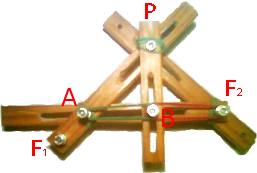
Il compasso è la esatta trasposizione nella realtà dello schema nella applicazione java. La differenza tra il segmento PF1 e PF2 è pari al segmento costante F1A. Per tracciare l’arco di iperbole è necessario, tenendo fissi i punti F1 e F2 ruotare attorno a F1 il punto A (e quindi il listello che congiunge F1 e P). Se PB rimane perpendicolare a AF essa è l’asse, la mediana e l’altezza del triangolo APF2 rispetto al lato AF2.  Il triangolo APF2 allora è isoscele e AP è uguale a PF. Ma, allora, F1P – F2P = F1A = costante . Nel modello che ho fatto io ho utilizzato due elastici dello stesso materiale e stessa lunghezza per tenere il punto B a metà tra A e F2.

I listelli di legno sono ciascuno ad un livello superiore all’altro, per poter scivolare liberamente. I livelli sono mantenuti da una serie di dadi inseriti nelle viti (non disponendo di un metodo migliore). Le fessure lungo i segmenti AP, PF, AB, permettono ad A,B e P di spostarsi e di tracciare l’arco d’iperbole.

Essendo più realistici, per realizzarne uno che funzioni veramente bene bisognerebbe farlo in metallo, con delle guide all’interno delle fessure per mantenere in sede gli elementi che scorrono, adeguatamente lubrificati. Si dovrebbe studiare un ingombro dei listelli tale da impedire quanto meno possibile il tracciamento della zona vicina all’asse trasverso. Per mantenere in posizione l’elemento PB sarebbe buona cosa usare due molle con una costante elastica di media grandezza e uguale tra le due, cosicché all’accorciarsi di una l’altra risponda simmetricamente e PB sia mantenuto perpendicolare. Infine sotto a P andrebbe inserito un supporto per inserire una mina da disegno.

Con lo strumento mostrato in figura sono riuscito a tracciare un arco di iperbole con eccentricità vicina ad 1, viste le dimensioni del triangolo APF2 (provare con l’applet java per credere!). Sarebbe bello poter ripetere l’esperimento… se mia madre nel frattempo non lo avesse scomposto in pezzi mettendo le viti con le viti, i dadi con i dadi, etc. Ho provveduto a rimontarlo pazientemente, cambiando i tempi in questo post (che avevo scritto prima) dal passato al presente.

Spero di averti fornito sufficienti informazioni. Sono rare da trovare le persone che si interessano di matematica… quindi, ti ringrazio per il tuo commento!! Se hai bisogno di sapere qualcos’altro scrivimelo!

A presto, ciao!